Maths enrichment in the East Midlands
My EPSRC research fellowship generously allows me to spend part of my time on outreach activities. If you’d like me speak at your school or event, please get in touch.
I also deliver maths sessions for on-campus events such as Inspiring Minds: STEM. If you’re a teacher wanting to arrange a campus visit at Loughborough, please contact the School and College Liaison.
Some topics I enjoy doing sessions on are:
The mathematics behind the rainbow. Oakham School published a lovely summary of this lecture after I delivered it there.- Combinatorial game theory. This workshop involves playing and analysing a few 2-player games with simple rules, but interesting strategies.
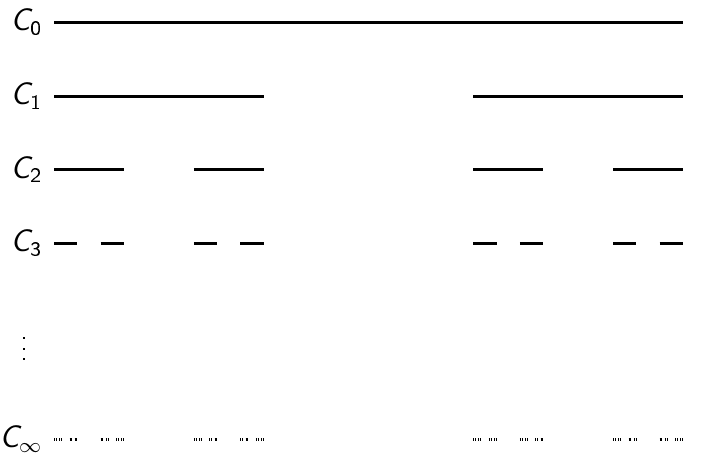Measuring infinity and fractal dimensions. This workshop tries to tame the strange concept that is infinity. We’ll discuss questions such as: How do we measure infinite sets? What does it mean when we say an object is 2-dimensional, 3-dimensional, etc? Are there objects of non-integer dimension?
Videos
In 2022 I produced a video about the pattern of waves making up the wake of a ship or a duck. This is a common topic in university-level fluid mechanics courses, but my intention was to give a fairly complete explanation without assuming any knowledge beyond high school maths:
This video received an honorable mention in the 2022 Summer of Math Exposition.
In October 2022 I appeared in a 24-hour maths game show, with a 30 minute segment on a 1-dimensional version of Conway’s Game of Life. You can still watch the recording and play with copy of the google spreadsheet.
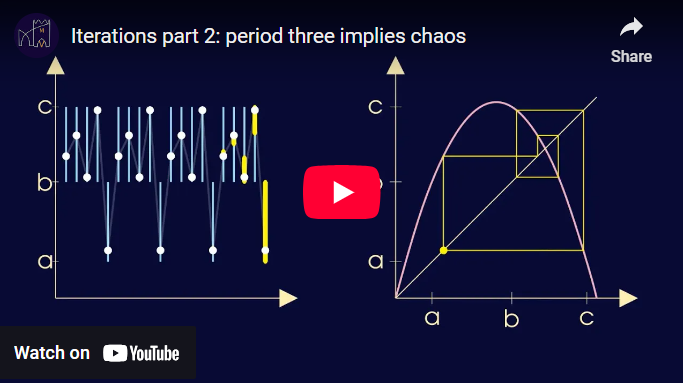
In 2024 I made a two-part video on iterations and chaos. The first part reviews some textbook material on the concept of iterations and how to visualise them. The second part has the more ambitious goals of understanding the titular claim of a 1975 paper by Tien-Yien Li and James A Yorke: period three implies chaos. The first part of this miniseries was my entry for that year’s community-run edition of the Summer of Math Exposition, #SoMEpi.
Blog posts
If you want to get an idea about my research area, have a look at blog posts below. There is a lot of maths between what is taught in school and the highly specialised topics of today’s research. In fact, these intermediate levels contain some exciting insights that aren’t too difficult to explain:
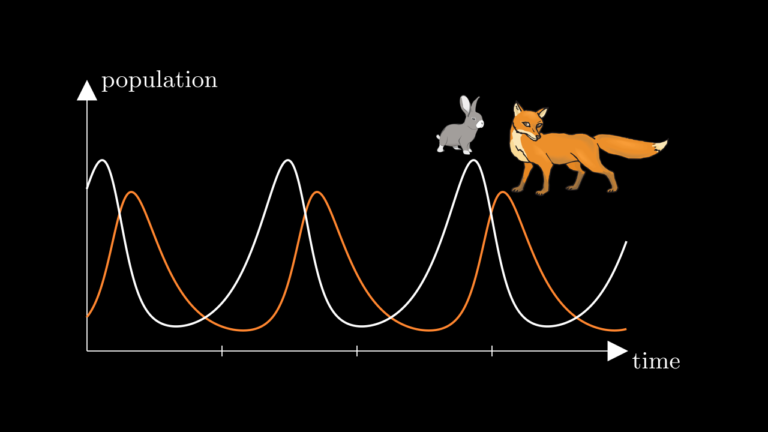
- Waves of predators
In mathematical biology, one of the simplest models of population dynamics is the Lotka-Volterra model. It is a system of two differential equations, modelling the interaction of the populations of two species: a predator and a prey. The mathematics behind it has a surprising connection to the dynamics of waves in a shallow canal. - Four different dynamical systems
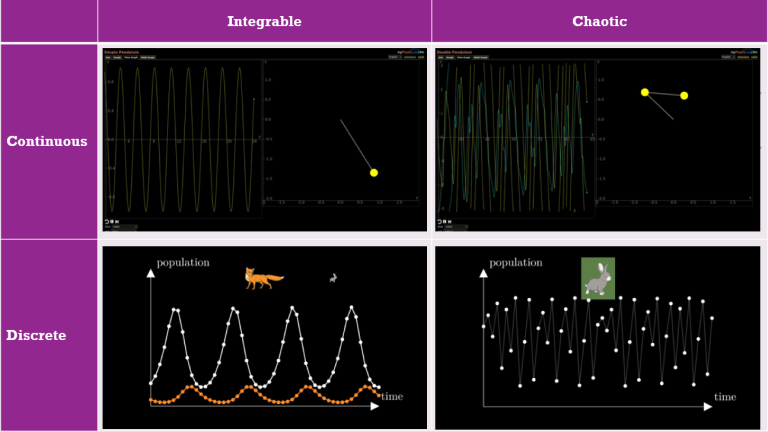
This multimedia post features four different dynamical systems to illustrate some properties of that relevant to my research: we’ll talk about the difference between “integrable” and “chaotic” dynamical systems, and the difference between “continuous-time” and “discrete-time” dynamical systems. - What is… a variational principle?
Variational principles play fundamental role in much of mathematical physics and are a key topic in my own research. That’s a lot to cover, so let’s start with a little story… - What is… an integrable system?
The oversimplified answer is that integrable systems are equations with a lot of structure. The kind of equations we are thinking about are differential equations, which describe change…
In print
Chalkdust is a “magazine for the mathematically curious”.
I wrote an article on Hamiltonian mechanics and Noether’s theorem for issue 15.