Variational principles play fundamental role in much of mathematical physics and are a key topic in my own research. That’s a lot to cover, so let’s start with a little story.
1. An injured cow and the laws of physics
On the morning of a hot summer’s day, a farmer noticed that one of his cows had broken its leg out in the field. The unfortunate the animal would not be able to move for a good while. To make sure the cow wouldn’t get dehydrated, the farmer had to bring it water from the stream bordering the field. While the farmer went to fetch a bucket, he thought about the best way to accomplish this task. What would be the shortest route he could take, that first visits the stream and then goes to the cow?

It is fairly obvious that the farmer should take a straight line to the river and then another straight line to the cow. We all learned in school that a straight line is the shortest route between two points. But there are still many ways to combine two straight lines into a suitable path. Which point on the river bank should the farmer go to in order to make the path as short as possible?
If you play around with different possibilities for a minute, you might be able to guess that both lines should make the same angle with the river bank. This simple condition, two angles being equal, is all that is needed to determine the shortest path.

A cow with a broken leg is unfortunate, but it could have been worse. What if the cow had fallen into the river? It won’t be able to get back onto dry land with its leg broken. Luckily the river isn’t too deep, so the clumsy animal won’t drown, but the farmer would have to wade into the river to help it.
Now what would be the fastest way for the farmer to reach the cow? The shortest path would be a straight line, but it is safe to assume that the farmer can run through the field faster than he can wade through the stream. So it’s worth taking a slightly longer path if a shorter part of it is in the water. The quickest route might look like this:

The problems our farmer is facing are examples of variational problems. We seek to minimize some quantity (distance or time travelled in these examples). If we have found the optimal solution, then any small variation of this solution will be slightly worse. This gives us a first explanation of the name variational problem.
The cows of physics
Why do we care about these problems? It wouldn’t really make a difference if the farmer takes a few seconds more to reach the cow, would it? And taking a slightly longer route probably wastes less time than overthinking the situation. So what’s all the fuss about?
It turns out that physics is a lot like a farmer trying to help his cow.
As a first example, consider a ray of light reflecting in a mirror. Out of all possible paths from the light source, via the mirror, to wherever the ray of light ends up, it will take the shortest. This is because the law of reflection says that the incident ray and the reflected ray will make the same angle with the mirror. And, as our farmer found out, equal angles create the shortest path.
Or is it the other way around? We might say that the law of reflection holds because light always takes the shortest path.
What about the cow in the river? Well, not just the farmer goes slower in water, so does light. It travels at “light speed” (about 300.000 km/s) in vacuum, marginally slower in air, and a lot slower in materials like water or glass. This matters because I lied to you earlier: light doesn’t necessarily take the shortest path, it takes the fastest path. If the speed of light were the same everywhere, this would make no difference. But if different materials are present, then the speed depends on where you are. So, if, for example, a ray of light enters water from the air, it makes a sudden turn. Just like our farmer did to reach his aquatic cow.

The phenomenon where light changes direction when it enters a different medium is called refraction. You might have learned the formula for the angle of refraction (known as Snell’s law) in your high school physics class:
\(\displaystyle n_i \sin \theta_i = n_R \sin \theta_R.\)
But you don’t need to understand this formula, because it just reflects the fact (no pun intended) that light takes the fastest route. If you want to do calculations, you need formulas. But if you want to understand what’s going on, the variational principle is even better. This particular variational principle, that light always takes the quickest path, is called Fermat’s principle.
As we will see below, light is no exception. Many more physical systems are described by variational principles. They are a cornerstone of every part of modern physics. Like many “laws” of physics, the law of reflection and Snell’s law are nothing but consequences of a simple variational principle.
2. Variational principles in statics
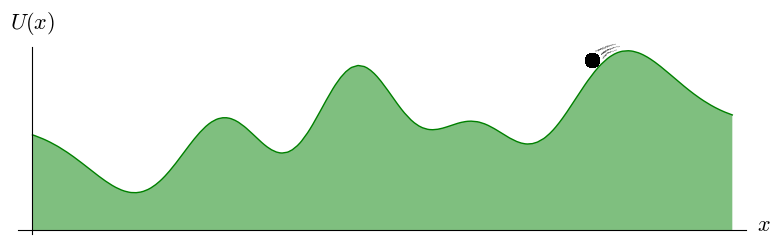
Consider an idyllic landscape of rolling hills…

No, wait. Scratch that! Picture these idealized 1-dimensional rolling hills:

The places where a ball would not immediately start rolling down the hill are those where the tangent line to the hill is horizontal: the tops of the hills and the bottoms of the valleys. In terms of calculus, these are the values of \(x\) where the derivative of \(U\) is zero:
\(\displaystyle \frac{\mathrm{d} U(x)}{\mathrm{d} x} = 0\)
This leads us to a second interpretation of the word variational. The derivative is the infinitesimal rate of change of a function. We can only have a minimum or a maximum if this rate of change, this variation, is zero. Variational problems look for a situation where the infinitesimal variation of some quantity is zero.
In our 1-dimensional landscape, there are eight such locations. There are eight equilibria, where a ball will stay at rest if there is no external force acting on it:

There is a clear difference between the orange balls and the blue balls. The orange ones are on top of hills. Each of them is at a local maximum of the function \(U\). This has the unfortunate consequence that as soon as the ball moves a tiny bit to either side, it will start rolling down the hill, away from its equilibrium. We call these kinds of equilibrium unstable. The blue balls, on the other hand, are at stable equilibria. If a blue ball gets a little kick, it will jiggle about its equilibrium, but eventually it will come back to rest at the same place.
In other words, the variational principle
\(\displaystyle \frac{\mathrm{d} U(x)}{\mathrm{d} x} = 0\)
determines all equilibria, but if we want to make sure we have a stable equilibrium, we need and additional condition. For example, we could require that the second derivative of \(U\) is positive,
\(\displaystyle \frac{\mathrm{d}^2 U(x)}{\mathrm{d}^2 x} > 0.\)
Both conditions combined guarantee that \(U\) has a local minimum at \(x\), or, that the ball will be in a stable equilibrium at position \(x\).
The function \(U\) is called the potential of the system. In this case, where gravity is the only force involved, the potential is essentially the height. In more complex systems, the potential will be a more complicated function of the variables of the system, but its use stays the same. Equilibria are found by applying the variational principle to the potential. Stable equilibria are the local minima of the potential.
3. Variational principles in dynamics
Finding the equilibria of a system is not the whole story. It is good to know where a system can be at rest, but often we also want to understand how it moves when it is not at rest. Miraculously, this is governed by variational principles too.
Suppose we want to keep track of a ball rolling through our 1-dimensional landscape.
We denote the position of the ball at time \(t\) by \(x(t)\). We can make a graph of position over time, so that \(x(t)\) traces out a curve in the \((x,t)\)-plane. Most such curves cannot be realized by a ball moving only under the influence of gravity. Those that can be, are called solutions of the system. For each initial position and velocity of the ball, there will be exactly one solution. But how do we find a solution?
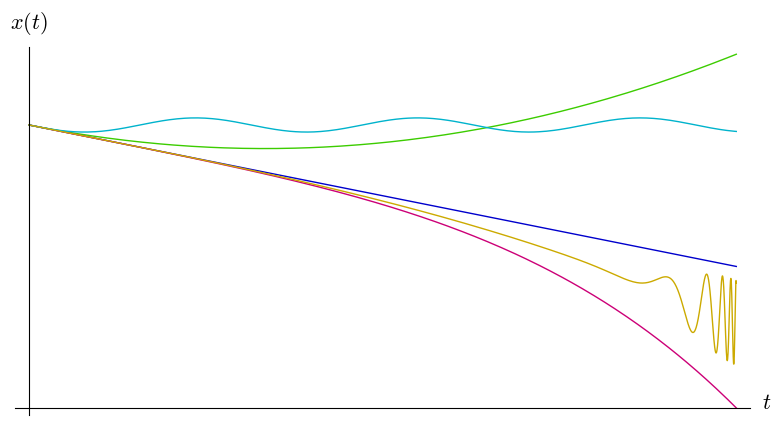
The most common approach is to use Newton’s second law: Force equals mass times acceleration. In a problem like this, at each location \(x\) the force \(F(x)\) is known. It is determined by the slope of the hill at that position. Acceleration is the second derivative of position with respect to time, so if we know the mass \(m\) of the ball, Newton’s second law gives us the formula
\(\displaystyle \frac{\mathrm{d}^2 x(t)}{\mathrm{d} t^2} = \frac{F(x)}{m}.\)
This is a (second order) differential equation. If the initial position \(x(0)\) and the initial velocity \(\frac{\mathrm{d} x(t)}{\mathrm{d} t} \Big|_{t=0}\) are given, then it can be solved to determine \(x(t)\) for all values of the time \(t\). (At least in theory. Only for relatively simple functions \(F(x)\) will it be possible to write this solution as a nice formula to calculate \(x(t)\).)
Instead of Newton’s second law, we can again use a variational principle. Compared to our previous examples, the quantity we want to minimize is a bit more complicated. Not to worry, though. Once again you don’t need to understand the formula to follow the rest of the text. We want to minimize
\(\displaystyle S[x] = \int_0^T \left( \left( \frac{m}{2} \frac{\mathrm{d} x(t)}{\mathrm{d} t} \right)^2 – U(x(t)) \right)\mathrm{d} t,\)
where the square brackets \([x]\) indicate that \(S\) depends on the function \(x\) as a whole, not just on a particular value \(x(t)\).
We look for minimizers of \(S\) in the following sense. Let the starting position (at time \(0\)) be \(a\) and the final position (at time \(T\)) \(b\), that is \(x(0) = a\) and \(x(T) = b\). Then \(x\) is a solution if \(S[x]\) is smaller than \(S[y]\) for any other function \(y\) with the same boundary values \(y(0) = a\) and \(y(T) = b\).
With some clever calculations, which involve taking variations of the function \(x\), one can see that the functions that minimize \(S\) are exactly those that satisfy Newton’s second law. Once again a famous law of physics turns out to be the consequence of a variational principle.
Variational principles are abundant in physics. I’ve only discussed simple examples here, but it turns out that almost all of modern physics can be formulated using variational principles. In fact the easiest way to describe a physical theory is often to write down the thing it minimizes.
Conserved quantities
The story does not end there. Instead of looking at functions with fixed boundary values to obtain Newton’s second Law, we could look only at functions satisfying Newton’s second law but leave the boundary values unspecified. Then similar “clever calculations” give some information about the boundary values. More specifically, they produce conserved quantities, like the energy of the system, which take the same value at the final time as at the initial time (and indeed at any time in between).
Exactly which conserved quantities come out of this procedure depends on the symmetries of the system. Noether’s theorem, named after early 20th century mathematician Emmy Noether, states that every symmetry corresponds to a conserved quantity. For example, if the system is translation invariant (e.g. billiard balls rolling on a plane) then its total momentum is conserved, and if it is rotationally invariant (e.g. planets orbiting the sun) then the angular momentum is conserved.
Knowing conserved quantities of a system helps to understand its dynamics on many levels. Whether you are looking for an exact solution, a numerical approximation, or a qualitative understanding of the behaviour, conserved quantities will always be of use. And if you have read “What is… an integrable system?“, you know that they are the key to a realm of very peculiar dynamical systems.
5. Sources and further reading
As with many concepts related to physics, a good place to start reading are the Feynman lectures: some relevant chapters are Optics: The Principle of Least Time and The Principle of Least Action.
Even though these physical insights (and the maths) have not changed since the Feynman lectures were published over half a century ago, the cutting edge of science communication has moved on. Nowadays there are excellent educational videos on subjects like this.
Most introductory texts on classical mechanics do not give variational principles the attention they deserve. A notable exception (and excellent book) is
- Levi, Mark. Classical mechanics with calculus of variations and optimal control: an intuitive introduction. American Mathematical Soc., 2014.
The example of the farmer and the cow is inspired on a problem in
- Stankova, Zvezdelina, and Tom Rike, eds. A Decade of the Berkeley Math Circle: The American Experience, Volume II. American Mathematical Soc., 2015.
