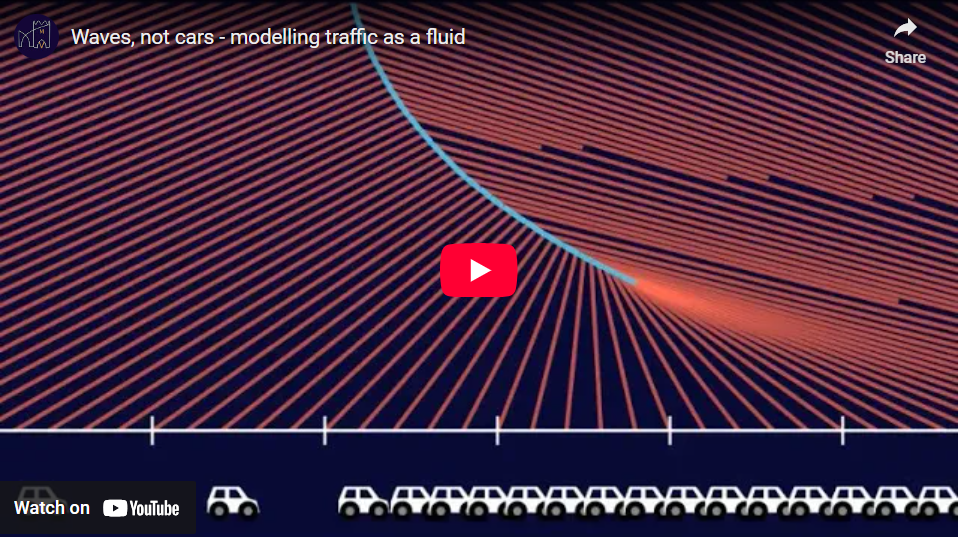
We give a visual introduction to the Lighthill-Whitham-Richards model of traffic flow and the method of characteristics. Through this model, we study examples of light and heavy motorway traffic, traffic lights, and the use of variable speed limits.
Full Video
Transcript with video snippets
Traffic as a fluid
An interesting way to think about traffic on a large scale is as a fluid. To model a fluid, we usually don’t think of individual molecules, but rather of macroscopic properties such as its density. In the same spirit, we can plot the density of the traffic and disregard the position of the individual cars.
So let’s draw a plot of the traffic density, which we denote by the greek letter \(\rho\) (rho).
As the cars move along the road, the plot of the density will change shape. Can we predict how it will change over time without modelling the actual cars?
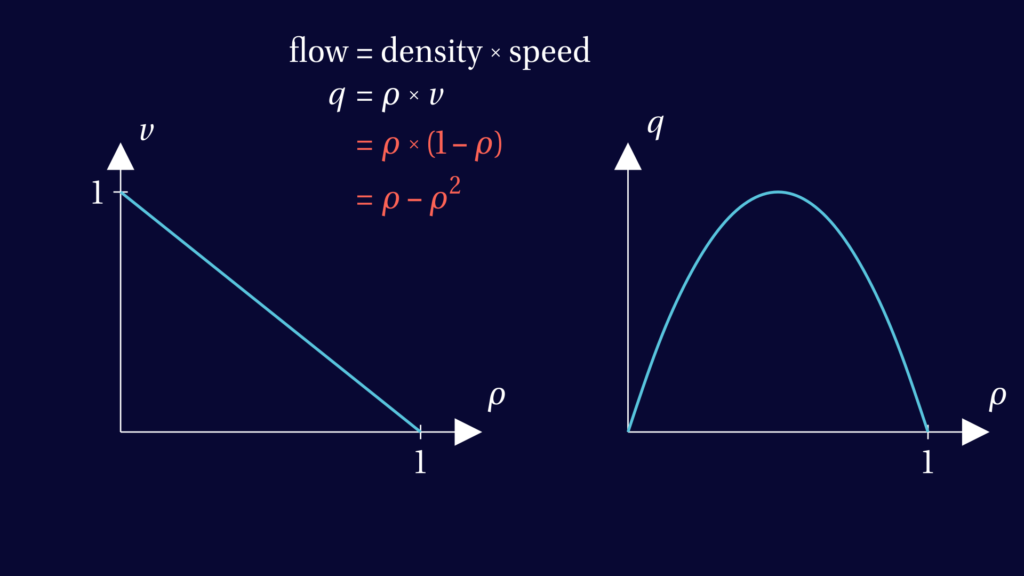
How do we model traffic if all we know is its density? A first step is to estimate how fast a car would be driving depending on the density of traffic it’s in. A fair assumption is that the denser the traffic is, the slower the cars will be. When traffic is very light, cars drive at their maximum speed, \( v_{max} \). When there is some traffic, cars drive at some slower speed. And when traffic is bumper to bumper, the cars don’t move at all.
So the graph of speed over density should slope down. It could take many different shapes, but for now, let’s take the simples possible option: a linear relation. The graph is a straight line, connecting a certain maximum speed when the density is zero, to a speed of zero when the density is maximal.
Let’s normalise density and speed. This means we choose use units of density and speed such that the maximum density and speed are both equal to one. This will simplify the formulas a little.
When analysing road traffic a key quantity is the flow \(q\): the amount of cars passing a fixed point per unit of time. The flow is equal to traffic density times the speed of the cars.
In the image below, formulas specific to our model are shown in red. In our model, the flow is a quadratic function of density. Its graph is a parabola which reaches its maximum at half the maximum density.
To turn these graphs of speed and flow into an equation for how the density evolves, all we need to do is look at the conservation of the number of cars. Our model should not create or remove cars. From this we can derive an equation for traffic flow.
To start the derivation, consider a short stretch of road, say between coordinates \(x\) and \(x+\varepsilon\). The total number of cars in this interval is approximately given the length of the interval \( \varepsilon \) times by the density \(\rho\).
The number of cars going into this interval per unit of time is given by the flow \(q(x)\). The number of cars leaving the interval in the same unit of time is the flow \(q(x+\varepsilon)\).
So the change in number of cars over time is given by the difference in flow at \(x\) and \(x+\varepsilon\): $$ \frac{\partial N}{\partial t} = q(x) – q(x+\varepsilon).$$

On the left hand side, we can plug in the formula for the number of cars, \( N = \varepsilon \rho \) to find $$ \varepsilon \frac{\partial \rho}{\partial t} = q(x) – q(x+\varepsilon).$$ Rearranging this gives $$ \frac{\partial \rho}{\partial t} + \frac{q(x+\varepsilon) – q(x)}{\varepsilon} = 0.$$
Letting epsilon tend to zero, we recognise the derivative of \(q\) with respect to \(x\). So, we find $$ \frac{\partial \rho}{\partial t} + \frac{\partial q}{\partial x} = 0.$$
With the chain rule, that turns into $$ \frac{\partial \rho}{\partial t} + \frac{\partial q}{\partial \rho} \frac{\partial \rho}{\partial x} = 0.$$
This equation relates the time-derivative of rho to its space derivative.
In our model, where \(q=\rho – \rho^2\), we have \( \frac{\partial q}{\partial \rho} = 1 – 2 \rho \).
Equations like this are called partial differential equations. The word “differential” indicates they involve derivatives, the word “partial” that there are derivatives with respect to several variables, here \(t\) and \(x\).
Method of characteristics
There is no general method to solve differential equations. But this one allows a nice trick, known as the method of characteristics.
The inspiration for this method comes from looking at a nearly constant traffic density with a small disturbance. We see that this small bump in the density moves with a constant speed. This speed is smaller than the speed of the cars!
In heavy traffic, the bump even moves backwards, against the direction of traffic.
This suggest that we should not be tracking how individual cars more, but how how waves of constant density move.
Imagine a helicopter flying over the densest bit of traffic. It does not follow an individual car – it follows a wave in traffic.
A space-time plot of the helicopter’s trajectory is called a characteristic. It is a line formed of points in space-time which all have the same traffic density.
Let’s draw many different characteristics, so that the space-time plot is almost filled with them. If we want to know the traffic density at a certain point with space-time coordinates \((x,t)\), all we have to do is to find a characteristic that goes through the point \((x,t)\). The density of that point will be equal to the density at time zero at the point where the characteristic originated.
Now, how do we know what the slope of a characteristic should be? Put differently, what speed the helicopter should be doing to make sure it sees the same density at all time?
Suppose the helicopter is flying at a certain speed c. The change it will observe in the traffic density rho is made up of two parts. One part is how rho itself is changing through time: \(\frac{\partial \rho}{\partial t}\). The other part is due to the helicopter’s motion: \( c \frac{\partial \rho}{\partial x}\) (once again, this is the chain rule at work). We want the helicopter to see a constant density, so we want this total change to be zero.
If we compare this to the partial differential equation for the traffic density rho, we see that the equations are almost the same. In particular, if $$ c =\frac{\partial q}{\partial \rho}$$ then the helicopter will see no change in density. This is exactly what we want, so this is the formula for the speed of the helicopter, or in more abstract terms, for the slope of a characteristic.

Recall that in our model, the flow q is a quadratic function of the traffic density rho. We find that the slope of the characteristic is \( 1 – 2 \rho \).
Reconstructing the density profile
Note that in light traffic, when \( \rho < \frac12 \), \(c\) is positive so characteristics slope forward. But in heavy traffic, when \( \rho > \frac12 \), \(c\) is negative so characteristics slope in the opposite direction.
Conversely, if we see the plot of characteristics, we can tell by their slope what traffic density they corresponds to. Suppose we want to reconstruct the plot of density at a certain time. First, we draw the horizontal line corresponding to this time in the space-time plot. Then, for each \(x\)-coordinate, we look at the slope \(c\) of the characteristic intersecting our line at that \(x\). From its slope we know the density. Sloping backwards means high density, sloping forwards means low density.
This way, we can read off the density profile from the plot of characteristics
When the initial traffic density is decreasing along the road, like this, the characteristics fan out. The gaps between characteristics are not a problem, because mathematically there are infinitely many of them. The gaps are there because we chose to draw only a few, so if we find a gap is getting too big, we can simply draw an additional characteristic in the gap. If you prefer, we could have drawn these extra characteristics from the start.
If the initial traffic density increases from left to right, the characteristics slope towards each other. At some point they intersect. If we have several characteristics going through the same point, we will find several different values when we try to reconstruct the density curve. So instead of the graph of a function, we get a meaningless S-shaped curve.
So we cannot have intersecting characteristics. Instead, when characteristics meet, they form a shock. This corresponds to a jump in the graph of density over \(x\).
The speed of the shock will have to be somewhere between the speeds of the intersecting characteristics.
The exact speed of the shock is determined by the fact that the flow into the shock should be the same as the flow out of the shock. But this is not the absolute flow q, but the flow as observed by someone moving with the shock.
Let’s say the speed of the shock is \(v\), then someone moving with the shock, staying just to the right of it, will observe a flow of
$$ q(\rho_\text{right}) – \rho_\text{right} v ,$$
where $\rho_{right}$ is the density the the right of the shock. Similarly, an observer following the shock on its left hand side will observe a flow of
$$ q(\rho_\text{left}) – \rho_\text{left} v .$$
Conservation of cars implies that these two flows must be equal, so we find that
$$ v = \frac{\rho_\text{left} – \rho_\text{right}}{q(\rho_\text{left}) – q(\rho_\text{right})} .$$
(This is known as the Rankine–Hugoniot condition.)
Examples on the motorway
Now we have all the tools to solve the traffic equation with the method of characteristics. Let’s look at a few examples.
First let’s consider big lump of traffic on an otherwise nearly empty road.
We see that a shock forms at the tail end of the queue. Initially, it moves backwards quite quickly, but then it slows down and the size of the jump in density starts to go down.
In real traffic, a shock is not concentrated in a single point like on our graph, but slightly spread out over a section of road. Furthermore, our model does not take into account that good drivers look far ahead to anticipate what will happen and adjust their driving accordingly. This will also help smooth out traffic compared to what we simulate in this model. But at a large scale, our model often gives a good indication.
Next, let’s look at a lump of denser traffic on a road that already has heavy traffic. Remember that heavy traffic means the density is more than half the maximum density and that the characteristics move backwards.
Again the shock that is formed moves backwards. And now it keeps going backwards. And the peak in density stays large. This is the situation when on a busy motorway, the traffic can be flowing nicely one moment, but the next instant you see a wall of brake lights moving towards you.
Let’s go back to light traffic, with a region of somewhat denser traffic, but remaining less than half the maximal density.
Maybe you’d expect the lump to be smoothed out without issue, but a shock is still formed. However, in light traffic like this, shocks moves forward, just like the characteristics. This means that from the perspective of a driver, the relative speed at which you approach the shock is much lower than in heavy traffic.
Combine this with the fact that real-life shocks will be a smoother version of what we simulate here, and it seems plausible that a shock in light traffic may not even be noticeable to the drivers. In any case it will be a much gentler affair than a shock in heavy traffic.
A traffic light
Next let’s look at a traffic light. When the light is on red, our model does not really apply to what is beyond the traffic light. But since no traffic can go past the red light, we could imagine the rest of the road to be completely full, with characteristics sloping backward. After all, a completely full road is also a way of modeling traffic that isn’t moving forward.
Unsurprisingly, a shock forms at the back of the growing queue.
When the light finally goes green, the initial traffic density is at its maxium on the left and zero on the right. This gives us the most extreme version of characteristics fanning out. The corresponding density plot after some time is a linear interpolation between the bumper-to-bumper queue on the left and the empty road on the right.
Note that the distances from the traffic light to the regions with full and zero density are the same. So if you imagine traffic going both ways, this would mean a car in the queue starts moving exactly when the first car going the other direction drives past it. Our model is way to simple to accurately capture such details of real life traffic. But still, when you are stopped at a pedestrian crossing, it does seem that you often start moving around the same time that the cars going the other way start coming past.
Active traffic management
let’s return to the motorway, where now the traffic density is half the maximal density on average, but fluctuates quite a lot. We see that many shocks are formed, and only very slowly do they decrease in size. It takes a very long time for the density to approach a uniform one.
However, in real life, sooner or later a careless driver will force another to slam on the brakes, creating new fluctuations, which then lead to new shocks. Is there anything the authorities could do to minimise the effect of such fluctuations on a fairly busy road?
There is. But it’s a measure that isn’t always welcomed by drivers. They could impose a speed limit.
Let’s go back to the basics of our model. So far, we assumed that the speed of the traffic is a linear function of traffic density. But if we impose a speed limit, then the graph changes as shown below. Here, the speed limit we chose is the speed cars would do at half the maximal density.
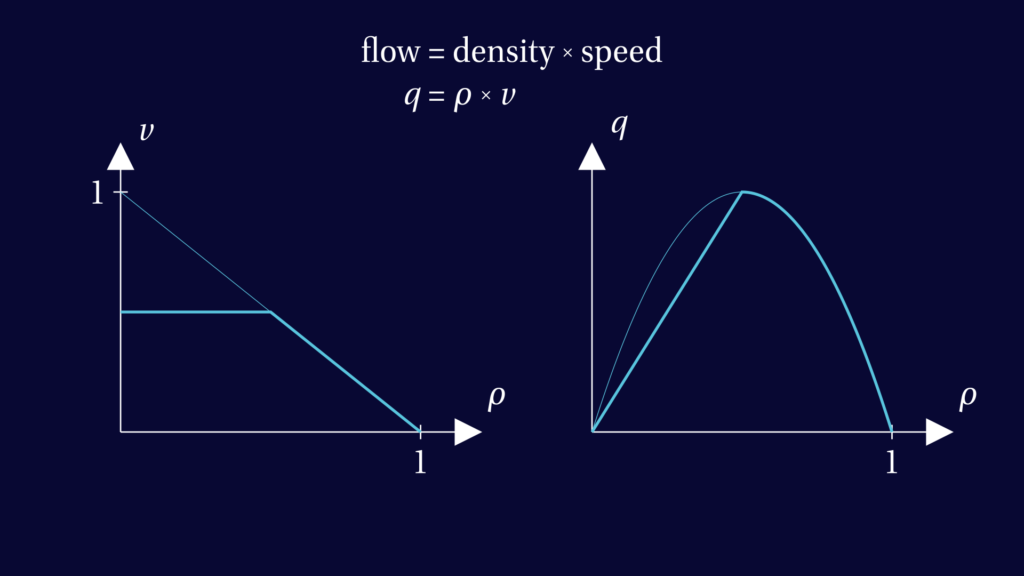
The graph of traffic flow, that is density times speed, now changes from a parabola to something that has a straight line as its first half.
This is notable, because the slope of this graph is what determines the slope of the characteristics. So with speed limit, all characteristics corresponding to light traffic will have the same slope.
Indeed, if traffic is light everywhere, the density profile now just moves to the right. Since all cars are driving the speed limit, the shape of the graph does not change, it just moves to the right uniformly.
But if we look back at the fluctuating traffic density from earlier, the shocks are dissipated much more quickly if the speed limit is imposed. And the traffic uniformises to a density of half the maximum quite quickly (which is the density at which the greatest possible flow is achieved).
Compare this to the simulation at the start of this section, with the same initial density and no speed limit. On the same time scale, there were still several shocks – many places where the traffic has to slam on the brakes.
So when there is a temporary speed limit on the motorway when there is no obstruction and traffic is flowing nicely, it is likely that the traffic density is such that big shocks would be forming if that speed limit wasn’t imposed. So it’s not that the speed limit is unnecessary because there’s no congestion. The speed limit has done its job and prevented queues forming!
Of course, to the road user it may appear as a useless speed limit. There’s no glory in prevention.
Or maybe, someone in a Birmingham office pressed the wrong button causing a single gantry on an empty A1M to show a 40 mile an hour speed limit. Who knows…
Notes
The Lighthill-Whitham-Richards model is also known as the kinematic wave model of traffic flow.
The original paper by Lighthill and Whitham is surprisingly readable:
Lighthill, Whitham (1955) On kinematic waves II. A theory of traffic flow on long crowded roads.
A textbook reference we found useful is:
Richard Haberman (1977) Mathematical Models: Mechanical Vibrations, Population Dynamics, and Traffic Flow. Prentice-Hall, New Yersey.
Another textbook, with more mathematical detail, is
Sandro Salsa, Gianmaria Verzini (2022) Partial Differential equations in Action. Fourth edition. Springer, Cham.
Optimising traffic flow through measures like variable speed limits is called active traffic management.
In theory, a shock will never disappear, but when a shock gets so weak that the difference in density on either side is negligible, we may for all practical purposes ignore it, which is why we stop drawing some of them on the space-time plot.
Manim code is available at https://github.com/mvermeeren/SoME4
Animations created with help of Matthew Truman.
This video is supported by the Engineering and Physical Sciences Research Council (EP/Y006712/1) and Loughborough University as part of my outreach work. Any mistakes or opinions in this video are my own.