This video on the mathematics behind rainbows communicates visually (without formulas) how the full story is more complicated, but also more beautiful, than “different wavelengths reflect at different angles”.
Below the full video you can find an edited transcript with the individual animations inserted into it. After that there is some additional material on double rainbows.
Full video
Transcript with video snippets
You may already know how a rainbow forms. A key part of the explanation is that sunlight is reflected in raindrops at an angle of about 42 degrees. So we see the reflected light if we are somewhere on this cone of reflected rays.
Put differently, we see reflected light from those droplets that appear to be on an arc, which is centered around the point opposite to the sun. And we don’t see reflected light from any droplets away from this arc.
The angle of reflection is slightly different for different wavelengths of light, which we see as different colours, so instead of one circular arc of reflected sunlight we see a rainbow.
It’s a nice explanation, and not entirely wrong, but the full truth is much more interesting.
Let’s look at what happens within a single raindrop. The sunlight (coming in from the left) is broken, or “refracted”, as it enters the raindrop. Then it is reflected on the inside of the raindrop and finally refracted again when leaving it.
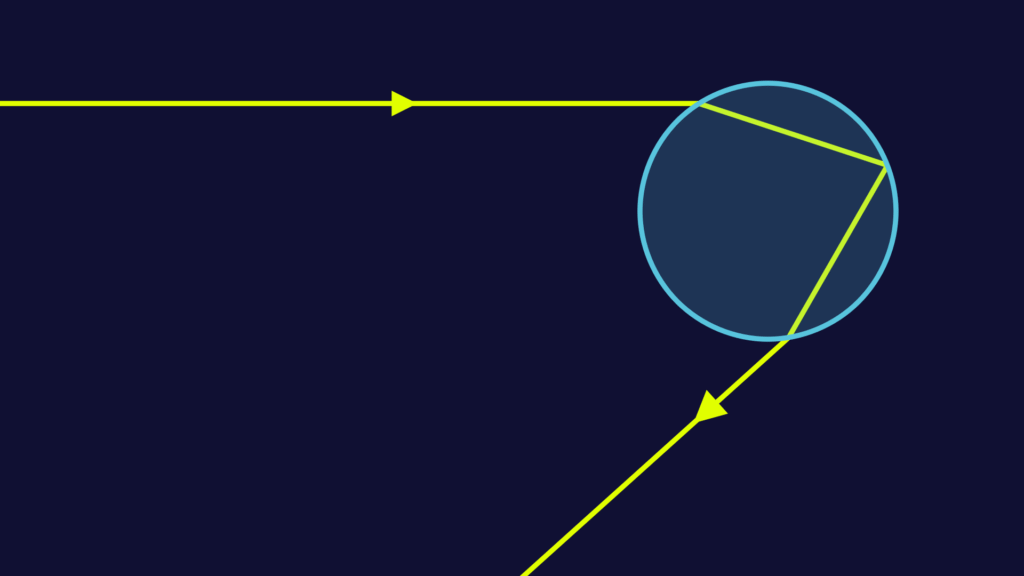
The breaking of light is related the fact that it moves more slowly in water than it does in air. (See this posts about variational principles.) The angle of refraction can be expressed using a formula called Snell’s law.
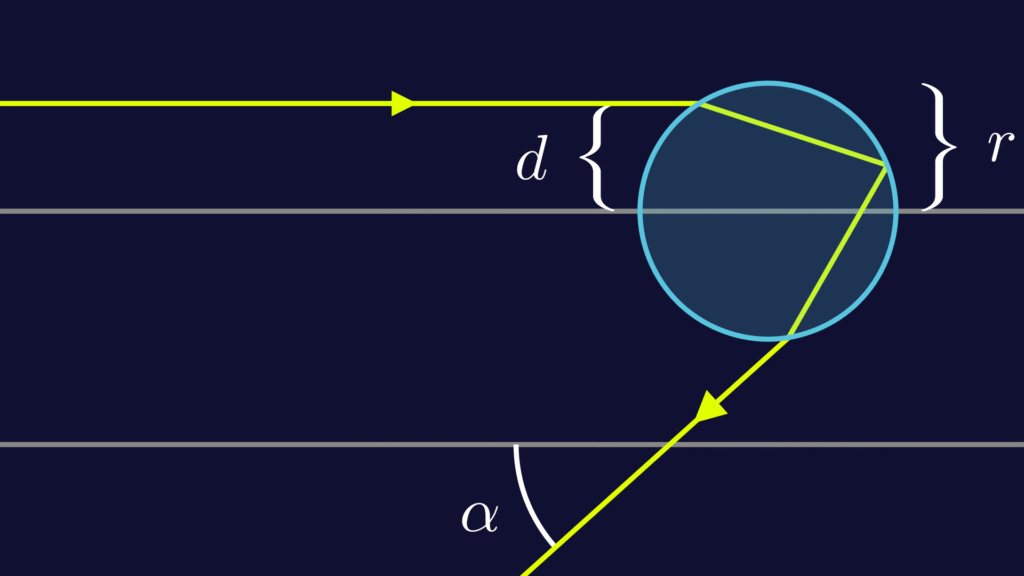
If you’re confident with trigonometry it’s a good exercise to calculate these angles. We won’t need exact formulas for this explanation to make sense, but if you manage to do this exercise, you’ll notice that the angle of the outbound ray depends on how far from the centre the inbound ray hits the raindrop. The angle, which we denote by \(\alpha\) (Greek letter alpha), depends on the distance \( d \) form the centre, as you can see in the animation below.
In hindsight, this shouldn’t be surprising. The angle certainly can’t always be 42°, because if the ray hits the droplet perfectly in the center, it will reflect back exactly the way it came.
It’s true that the angles depend a little on the wavelength of the light too, but the effect of changing the colour is much smaller than the effect of moving to or from the centre.
Let’s focus again on a single colour and draw a graph to visualise the dependence of the angle \(\alpha\) on the distance \(d\). We start at \(d=0\), which means the ray hits at the centre and the angle is zero too. When \(d\) increases, at first the angle \(\alpha\) increases too. But after a while the graphs flattens out and the angle reaches a maximum. When the ray moves even further from the center, the angle actually becomes smaller again.
We see that, depending on the value of \(d\), reflection is possible at any angle up to about 42 degrees.
This is a bit strange, because this seems to imply that a rainbow would be a filled disk in the sky, rather than a circular arc.

Another way to visualise this, is to look at lot of equally spaced incoming rays hitting our droplet. We see that a disproportionate amount of them reflect at or near the maximum angle.
On the graph these rays correspond to input values evenly distributed over the horizontal axis. After moving them to their output values, we see that the outputs are concentrated near the maximum value. This effect becomes more obvious when we consider more inputs rays.
Up to now we’ve only used light of a single wavelength (ie. of a single colour). The graphs for different wavelengths look very similar, with the notable difference that the maximum value is slightly different for each one. Hence the vertical bars representing our outputs will be of slightly different height, depending on the colour
Sunlight is a mixture of different colours. So what we really want to know is what these coloured bars look like when they overlap. This will give us a visual indication of how much light of which colour is reflected at each angle.
(People say the rainbow has 7 colours, but actually it has infinitely many. We’re using 6 here, which is a reasonable approximation.)
Finally, the light does not only get reflected vertically, but in all directions, so to visualise how the reflections actually look, we need to rotate this coloured bar around its lowest point, which corresponds to the angle zero and would be exactly opposite to where the sun is in the sky.
And voila. Here’s our rainbow. We see the bright arcs of differently coloured light, with a faint mix of colours inside of it, which looks more or less white to us.
So next time you see a shiny rainbow, see if you can tell that the inside of it is slightly brighter than the outside.
Additional material: double rainbows
So far we’ve assumed that the ray reflects exactly once inside the droplet. It could reflect multiple times, or leave the droplet without reflecting.
The most important of these cases is when the ray reflects twice inside the droplet. Let’s have a look at how different incoming rays get deflected in this case.
Again we can construct the graph of outgoing angle as a function of the distance \(d\).
This graph has a minimum instead of a maximum, but this will cause the same kind of concentration of outputs near the minimum angle.
Now let’s combine the graph for two reflections with the one for a single reflection and construct the rainbow…
We get a double rainbow with a dark band between the two bows.
In theory, there could also be a triple rainbow, quadruple rainbow, and so one. But with each additional reflection, the rainbow will get dimmer. In addition, the position of the theoretical third rainbow would be quite close to where the sun is, so in practice there is very little chance of ever seeing it.
YouTube video published on 22 August 2021
This page was updated 19 September 2025
The content of this page can be reused with attribution under the CC BY 4.0 license.

