Mats Vermeeren – Mats Vermeeren

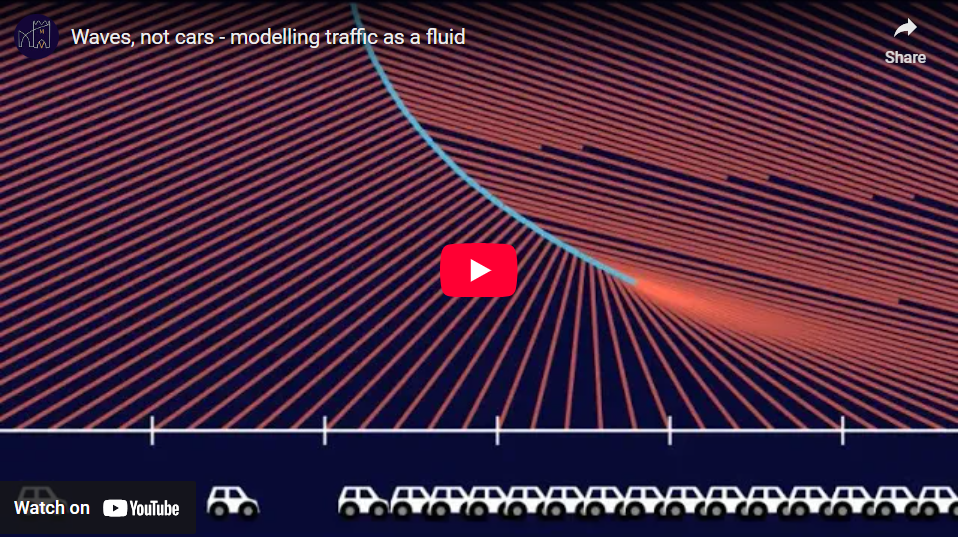
Waves, not cars – modelling traffic as a fluid

We give a visual introduction to the Lighthill-Whitham-Richards model of traffic flow and the method of characteristics. Through this model, we study examples of light and heavy motorway traffic, traffic lights, and the use of variable speed limits.

Full Video

Transcript with video snippets

Traffic as a fluid

An interesting way to think about traffic on a large scale is as a fluid. To model a fluid, we usually don’t think of individual molecules, but rather of macroscopic properties such as its density. In the same spirit, we can plot the density of the traffic and disregard the position of the individual cars.

So let’s draw a plot of the traffic density, which we denote by the greek letter $\rho$ (rho).

As the cars move along the road, the plot of the density will change shape. Can we predict how it will change over time without modelling the actual cars?

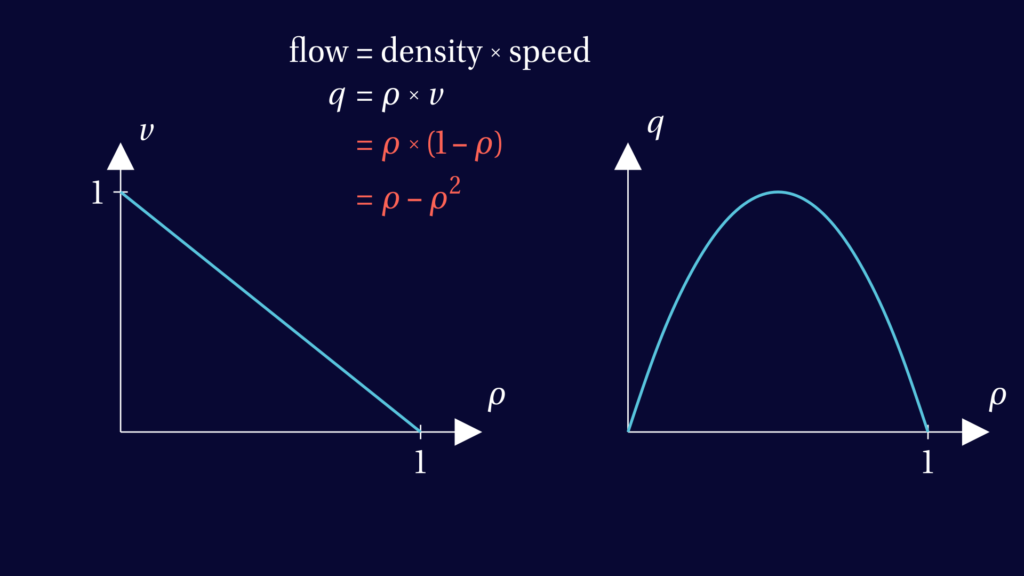
How do we model traffic if all we know is its density? A first step is to estimate how fast a car would be driving depending on the density of traffic it’s in. A fair assumption is that the denser the traffic is, the slower the cars will be. When traffic is very light, cars drive at their maximum speed, $ v_{max} $. When there is some traffic, cars drive at some slower speed. And when traffic is bumper to bumper, the cars don’t move at all.

So the graph of speed over density should slope down. It could take many different shapes, but for now, let’s take the simples possible option: a linear relation. The graph is a straight line, connecting a certain maximum speed when the density is zero, to a speed of zero when the density is maximal.
Let’s normalise density and speed. This means we choose use units of density and speed such that the maximum density and speed are both equal to one. This will simplify the formulas a little.

When analysing road traffic a key quantity is the flow $q$: the amount of cars passing a fixed point per unit of time. The flow is equal to traffic density times the speed of the cars.

In the image below, formulas specific to our model are shown in red. In our model, the flow is a quadratic function of density. Its graph is a parabola which reaches its maximum at half the maximum density.

To turn these graphs of speed and flow into an equation for how the density evolves, all we need to do is look at the conservation of the number of cars. Our model should not create or remove cars. From this we can derive an equation for traffic flow.

To start the derivation, consider a short stretch of road, say between coordinates $x$ and $x+\varepsilon$. The total number of cars in this interval is approximately given the length of the interval $ \varepsilon $ times by the density $\rho$.

The number of cars going into this interval per unit of time is given by the flow $q(x)$. The number of cars leaving the interval in the same unit of time is the flow $q(x+\varepsilon)$.

So the change in number of cars over time is given by the difference in flow at $x$ and $x+\varepsilon$: $$ \frac{\partial N}{\partial t} = q(x) – q(x+\varepsilon).$$

On the left hand side, we can plug in the formula for the number of cars, $ N = \varepsilon \rho $ to find $$ \varepsilon \frac{\partial \rho}{\partial t} = q(x) – q(x+\varepsilon).$$ Rearranging this gives $$ \frac{\partial \rho}{\partial t} + \frac{q(x+\varepsilon) – q(x)}{\varepsilon} = 0.$$

Letting epsilon tend to zero, we recognise the derivative of $q$ with respect to $x$. So, we find $$ \frac{\partial \rho}{\partial t} + \frac{\partial q}{\partial x} = 0.$$

With the chain rule, that turns into $$ \frac{\partial \rho}{\partial t} + \frac{\partial q}{\partial \rho} \frac{\partial \rho}{\partial x} = 0.$$

This equation relates the time-derivative of rho to its space derivative.

In our model, where $q=\rho – \rho^2$, we have $ \frac{\partial q}{\partial \rho} = 1 – 2 \rho $.

Equations like this are called partial differential equations. The word “differential” indicates they involve derivatives, the word “partial” that there are derivatives with respect to several variables, here $t$ and $x$.

Method of characteristics

There is no general method to solve differential equations. But this one allows a nice trick, known as the method of characteristics.

The inspiration for this method comes from looking at a nearly constant traffic density with a small disturbance. We see that this small bump in the density moves with a constant speed. This speed is smaller than the speed of the cars!

In heavy traffic, the bump even moves backwards, against the direction of traffic.

This suggest that we should not be tracking how individual cars more, but how how waves of constant density move.

Imagine a helicopter flying over the densest bit of traffic. It does not follow an individual car – it follows a wave in traffic.

A space-time plot of the helicopter’s trajectory is called a characteristic. It is a line formed of points in space-time which all have the same traffic density.

Let’s draw many different characteristics, so that the space-time plot is almost filled with them. If we want to know the traffic density at a certain point with space-time coordinates $(x,t)$, all we have to do is to find a characteristic that goes through the point $(x,t)$. The density of that point will be equal to the density at time zero at the point where the characteristic originated.

Now, how do we know what the slope of a characteristic should be? Put differently, what speed the helicopter should be doing to make sure it sees the same density at all time?

Suppose the helicopter is flying at a certain speed c. The change it will observe in the traffic density rho is made up of two parts. One part is how rho itself is changing through time: $\frac{\partial \rho}{\partial t}$. The other part is due to the helicopter’s motion: $ c \frac{\partial \rho}{\partial x}$ (once again, this is the chain rule at work). We want the helicopter to see a constant density, so we want this total change to be zero.

If we compare this to the partial differential equation for the traffic density rho, we see that the equations are almost the same. In particular, if $$ c =\frac{\partial q}{\partial \rho}$$ then the helicopter will see no change in density. This is exactly what we want, so this is the formula for the speed of the helicopter, or in more abstract terms, for the slope of a characteristic.

Recall that in our model, the flow q is a quadratic function of the traffic density rho. We find that the slope of the characteristic is $ 1 – 2 \rho $.

Reconstructing the density profile

Note that in light traffic, when $ \rho < \frac12 $, $c$ is positive so characteristics slope forward. But in heavy traffic, when $ \rho > \frac12 $, $c$ is negative so characteristics slope in the opposite direction.

Conversely, if we see the plot of characteristics, we can tell by their slope what traffic density they corresponds to. Suppose we want to reconstruct the plot of density at a certain time. First, we draw the horizontal line corresponding to this time in the space-time plot. Then, for each $x$-coordinate, we look at the slope $c$ of the characteristic intersecting our line at that $x$. From its slope we know the density. Sloping backwards means high density, sloping forwards means low density.

This way, we can read off the density profile from the plot of characteristics

When the initial traffic density is decreasing along the road, like this, the characteristics fan out. The gaps between characteristics are not a problem, because mathematically there are infinitely many of them. The gaps are there because we chose to draw only a few, so if we find a gap is getting too big, we can simply draw an additional characteristic in the gap. If you prefer, we could have drawn these extra characteristics from the start.

If the initial traffic density increases from left to right, the characteristics slope towards each other. At some point they intersect. If we have several characteristics going through the same point, we will find several different values when we try to reconstruct the density curve. So instead of the graph of a function, we get a meaningless S-shaped curve.

So we cannot have intersecting characteristics. Instead, when characteristics meet, they form a shock. This corresponds to a jump in the graph of density over $x$.

The speed of the shock will have to be somewhere between the speeds of the intersecting characteristics.

The exact speed of the shock is determined by the fact that the flow into the shock should be the same as the flow out of the shock. But this is not the absolute flow q, but the flow as observed by someone moving with the shock.

Let’s say the speed of the shock is $v$, then someone moving with the shock, staying just to the right of it, will observe a flow of
$$ q(\rho_\text{right}) – \rho_\text{right} v ,$$
where $\rho_{right}$ is the density the the right of the shock. Similarly, an observer following the shock on its left hand side will observe a flow of
$$ q(\rho_\text{left}) – \rho_\text{left} v .$$
Conservation of cars implies that these two flows must be equal, so we find that
$$ v = \frac{\rho_\text{left} – \rho_\text{right}}{q(\rho_\text{left}) – q(\rho_\text{right})} .$$
(This is known as the Rankine–Hugoniot condition.)

Examples on the motorway

Now we have all the tools to solve the traffic equation with the method of characteristics. Let’s look at a few examples.

First let’s consider big lump of traffic on an otherwise nearly empty road.

We see that a shock forms at the tail end of the queue. Initially, it moves backwards quite quickly, but then it slows down and the size of the jump in density starts to go down.

In real traffic, a shock is not concentrated in a single point like on our graph, but slightly spread out over a section of road. Furthermore, our model does not take into account that good drivers look far ahead to anticipate what will happen and adjust their driving accordingly. This will also help smooth out traffic compared to what we simulate in this model. But at a large scale, our model often gives a good indication.

Next, let’s look at a lump of denser traffic on a road that already has heavy traffic. Remember that heavy traffic means the density is more than half the maximum density and that the characteristics move backwards.

Again the shock that is formed moves backwards. And now it keeps going backwards. And the peak in density stays large. This is the situation when on a busy motorway, the traffic can be flowing nicely one moment, but the next instant you see a wall of brake lights moving towards you.

Let’s go back to light traffic, with a region of somewhat denser traffic, but remaining less than half the maximal density.

Maybe you’d expect the lump to be smoothed out without issue, but a shock is still formed. However, in light traffic like this, shocks moves forward, just like the characteristics. This means that from the perspective of a driver, the relative speed at which you approach the shock is much lower than in heavy traffic.

Combine this with the fact that real-life shocks will be a smoother version of what we simulate here, and it seems plausible that a shock in light traffic may not even be noticeable to the drivers. In any case it will be a much gentler affair than a shock in heavy traffic.

A traffic light

Next let’s look at a traffic light. When the light is on red, our model does not really apply to what is beyond the traffic light. But since no traffic can go past the red light, we could imagine the rest of the road to be completely full, with characteristics sloping backward. After all, a completely full road is also a way of modeling traffic that isn’t moving forward.

Unsurprisingly, a shock forms at the back of the growing queue.

When the light finally goes green, the initial traffic density is at its maxium on the left and zero on the right. This gives us the most extreme version of characteristics fanning out. The corresponding density plot after some time is a linear interpolation between the bumper-to-bumper queue on the left and the empty road on the right.

Note that the distances from the traffic light to the regions with full and zero density are the same. So if you imagine traffic going both ways, this would mean a car in the queue starts moving exactly when the first car going the other direction drives past it. Our model is way to simple to accurately capture such details of real life traffic. But still, when you are stopped at a pedestrian crossing, it does seem that you often start moving around the same time that the cars going the other way start coming past.

Active traffic management

let’s return to the motorway, where now the traffic density is half the maximal density on average, but fluctuates quite a lot. We see that many shocks are formed, and only very slowly do they decrease in size. It takes a very long time for the density to approach a uniform one.

However, in real life, sooner or later a careless driver will force another to slam on the brakes, creating new fluctuations, which then lead to new shocks. Is there anything the authorities could do to minimise the effect of such fluctuations on a fairly busy road?

There is. But it’s a measure that isn’t always welcomed by drivers. They could impose a speed limit.

Let’s go back to the basics of our model. So far, we assumed that the speed of the traffic is a linear function of traffic density. But if we impose a speed limit, then the graph changes as shown below. Here, the speed limit we chose is the speed cars would do at half the maximal density.

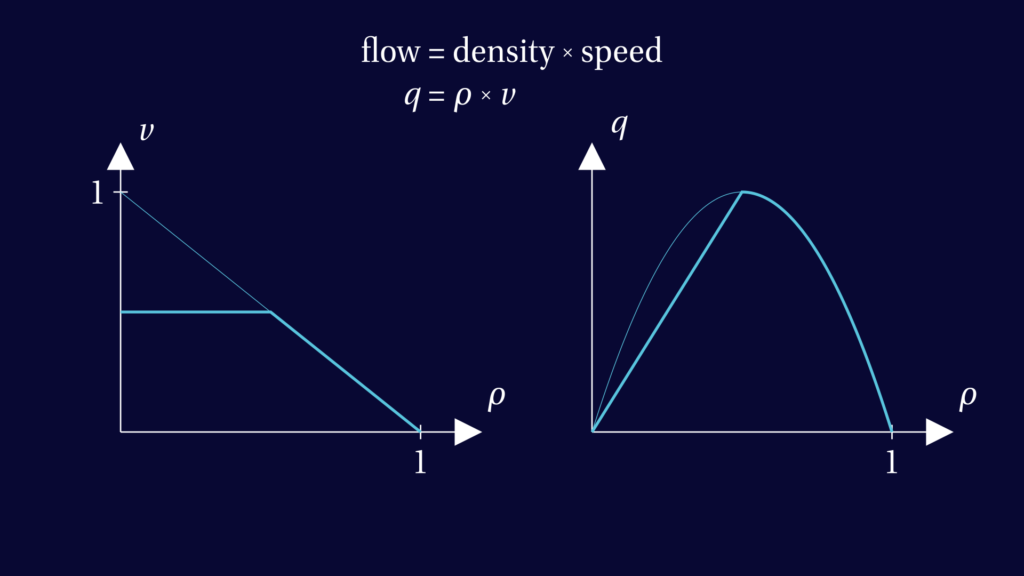
The graph of traffic flow, that is density times speed, now changes from a parabola to something that has a straight line as its first half.

This is notable, because the slope of this graph is what determines the slope of the characteristics. So with speed limit, all characteristics corresponding to light traffic will have the same slope.

Indeed, if traffic is light everywhere, the density profile now just moves to the right. Since all cars are driving the speed limit, the shape of the graph does not change, it just moves to the right uniformly.

But if we look back at the fluctuating traffic density from earlier, the shocks are dissipated much more quickly if the speed limit is imposed. And the traffic uniformises to a density of half the maximum quite quickly (which is the density at which the greatest possible flow is achieved).

Compare this to the simulation at the start of this section, with the same initial density and no speed limit. On the same time scale, there were still several shocks – many places where the traffic has to slam on the brakes.

So when there is a temporary speed limit on the motorway when there is no obstruction and traffic is flowing nicely, it is likely that the traffic density is such that big shocks would be forming if that speed limit wasn’t imposed. So it’s not that the speed limit is unnecessary because there’s no congestion. The speed limit has done its job and prevented queues forming!

Of course, to the road user it may appear as a useless speed limit. There’s no glory in prevention.

Or maybe, someone in a Birmingham office pressed the wrong button causing a single gantry on an empty A1M to show a 40 mile an hour speed limit. Who knows…

Notes

The Lighthill-Whitham-Richards model is also known as the kinematic wave model of traffic flow.

The original paper by Lighthill and Whitham is surprisingly readable:
Lighthill, Whitham (1955) On kinematic waves II. A theory of traffic flow on long crowded roads.

A textbook reference we found useful is:
Richard Haberman (1977) Mathematical Models: Mechanical Vibrations, Population Dynamics, and Traffic Flow. Prentice-Hall, New Yersey.

Another textbook, with more mathematical detail, is
Sandro Salsa, Gianmaria Verzini (2022) Partial Differential equations in Action. Fourth edition. Springer, Cham.

Optimising traffic flow through measures like variable speed limits is called active traffic management.

In theory, a shock will never disappear, but when a shock gets so weak that the difference in density on either side is negligible, we may for all practical purposes ignore it, which is why we stop drawing some of them on the space-time plot.

Manim code is available at https://github.com/mvermeeren/SoME4

Animations created with help of Matthew Truman.

This video is supported by the Engineering and Physical Sciences Research Council (EP/Y006712/1) and Loughborough University as part of my outreach work. Any mistakes or opinions in this video are my own.

Iterations and chaos

A two-part video on iterations and chaos. The first part reviews some textbook material on the concept of iterations and how to visualise them. The second part has the more ambitious goals of understanding the titular claim of a 1975 paper by Tien-Yien Li and James A Yorke: period three implies chaos.

Waves of predators

In mathematical biology, one of the simplest models of population dynamics is the Lotka-Volterra model. It is a system of two differential equations, modelling the interaction of the populations of two species: a predator and a prey. The mathematics behind it has a surprising connection to the dynamics of waves in a shallow canal.

This blog post originally appeared as my pitch for the Big Internet Math-Off 2024

The Lotka-Volterra predator-prey model

Imagine a population of cute rabbits living in a large grassland. There’s plenty of food to be found, so, rabbits being rabbits, you may expect the population size to grow exponentially. The population size at time $ t $ may be approximated by a function $ x(t) $ satisfying the differential equation
$$ \frac{\mathrm d x}{\mathrm d t} = \alpha x $$
for some constant $ \alpha > 0 $.

Unfortunately for our long-eared friends, a group of foxes has moved into the grassland. Let’s denote the size of the fox population by $ y(t) $. This introduces a new term to the differential equation:
$$ \frac{\mathrm d x}{\mathrm d t} = \alpha x – \beta x y \,, $$
where $ \beta > 0 $ is another constant. The new term slows down the growth of the rabbit population. It is proportional to the product $ x y $ of both population sizes. This reflects the observations that (i) if there are more foxes, they will eat more rabbits and (ii) if there are more rabbits, the same number of foxes will catch more rabbits, relying less on other food sources.

If we factorise the right hand side, the differential equation reads

$$ \frac{\mathrm d x}{\mathrm d t} = (\alpha – \beta y) x \,. \tag{1}$$
There is a similar differential equation for the population size of the foxes:
$$ \frac{\mathrm d y}{\mathrm d t} = (\delta x – \gamma) y \,, \tag{2}$$
where $ \gamma $ and $ \delta $ are positive constants. If the expression in brackets were constant, this would again give exponential growth (or decay). The dependence on $ x $ of this factor means the growth of the fox population is faster the more rabbits there are. But if there are too few rabbits (not enough food), then $ \delta x – \gamma $ becomes negative and the fox population decays.

The system of equations (1)-(2) is known as the Lotka-Volterra predator-prey model. For most biological applications it is too simple to capture the real population dynamics, but it’s mathematical structure is quite pleasing. A typical solution looks like this:

A plot showing population over time for rabbits and foxes. The graphs are periodic and the fox population always peaks slightly after the rabbit population. — Population over time of rabbits (white) and foxes (orange) for a typical solution to the Lotka-Volterra equations.

The populations fluctuate in a periodic way: after a certain amount of time, the population sizes are exactly what they were in the beginning. Then they repeat the same rise and fall over and over again.

The periodicity can be explained by the fact that the system has a conserved quantity
$$ F(x,y) = \alpha \log(y) – \beta y + \gamma \log(x) – \delta x \,. $$
“Conserved quantity” means exactly what it says on the tin: $ F(x,y) $ does not change over time. You can check that
$$ \frac{d F}{d t} = \frac{\partial F}{\partial x} \frac{d x}{d t} + \frac{\partial F}{\partial y} \frac{d y}{d t} $$
is zero by virtue of the Lotka-Volterra equations (1)-(2). We can also confirm this graphically by drawing a contour plot of $ F(x,y) $ and comparing it to the curve that a solution traces in the $ (x,y) $-plane. We see that the solution stays on one of the level sets of $ F $:

A plot showing the population of rabbits on the x-axis and the population of foxes on the y-axis. The contour lines of F are closed curves nested within each other. The path traced by a solution coincides with one of the contour lines. — Contour lines of the conserved quantify F (yellow) and the path traced by a solution to the Lotka-Volterra equations (white).

The Volterra Chain

To keep our equations simple, let’s set all the constants equal to 1 and consider the system
$$\begin{cases}
\displaystyle \frac{\mathrm d x}{\mathrm d t} = (1 – y) x \,, \\
\displaystyle \frac{\mathrm d y}{\mathrm d t} = (x – 1) y \,.
\end{cases}$$

What if we add another species to the ecosystem? One that eats foxes. If we denote its population size by $ z $, then the system of equations becomes
$$\begin{cases}
\displaystyle \frac{\mathrm d x}{\mathrm d t} = (1 – y) x \,, \\
\displaystyle \frac{\mathrm d y}{\mathrm d t} = (x – z) y \,, \\
\displaystyle \frac{\mathrm d z}{\mathrm d t} = (y – 1) z \,.
\end{cases}$$
Now why stop at three? Consider a whole sequence of species $ q_1, \ldots, q_n $, such that each species eats the species whose index is one less. This leads to the system of equations
$$\begin{cases}
\displaystyle \frac{\mathrm d q_1}{\mathrm d t} = (1 – q_2) q_1 \,, \\
\displaystyle \frac{\mathrm d q_i}{\mathrm d t} = (q_{i-1} – q_{i+1}) q_i \qquad \text{ for } i = 2, \ldots, n-1 \,, \\
\displaystyle \frac{\mathrm d q_n}{\mathrm d t} = (q_{n-1} – 1) q_n \,.
\end{cases}$$
This system of equations is known as the Volterra chain. As a biological model, it probably isn’t very realistic. It assumes that there is a long food chain where each species exclusively eats the one just below it. But this isn’t a biology-off, it’s a math-off. And mathematically, the Volterra chain is an interesting object.

The Volterra Chain is a discrete analogue of certain wave equations, where the continuous space variable of a wave equation is replaced by the discrete sequence of species forming our food chain. If we take a large number of species $n$, it is not hard to see the wavy nature of this system:

A sequence of many plots of population over time. Each graph has a peak at a slightly later time than the previous graph. The graphs are arranged in a 3D perspective such the peaks look like a travelling wave. — A disturbance in the population sizes of many species (numbered 1,2,3,…) propagates like a wave.

In this picture we started with a spike in population of species number 1, the lowest on the food chain. This perturbation ripples through the other species like a wave. After the wave has passed, population numbers settle back into the equilibrium.

Such a solitary wave, one that travels along without changing its shape, is called a soliton.

Solitons and water waves

There are several ways to approach the theory of soliton equations, but on some level they all come back to our observation that the two-species Lotka-Volterra model has a conserved quantity. Soliton equations have a lot of conserved quantities (infinitely many in fact). And it turns out that if you have an equation that conserves many different abstract things, you can deduce that it will also conserve some very tangible features, like the shape of a traveling wave.

Another equation that famously exhibits solitons is the Korteweg-de Vries (KdV) equation, modelling waves in a shallow canal. You can see an example of a KdV soliton in this video from the Scripps Institution of Oceanography:

The mathematical description of the solitons and other features of the KdV equation mimics that of the Volterra chain. In fact, you can consider the KdV equation as a limit of the Volterra chain with infinitely many species!

Four different dynamical systems

This multimedia post features four different dynamical systems to illustrate some properties of that relevant to my research: we’ll talk about the difference between “integrable” and “chaotic” dynamical systems, and the difference between “continuous-time” and “discrete-time” dynamical systems.

[Some phrases in the text can be expanded for :more info.]

Introduction

This is an extended write-up of a five-minute talk I gave to an interdisciplinary audience at Loughborough University’s 2022 Research Conference. It features four different :dynamical systems to illustrate some properties of dynamical systems relevant to my research. In particular, we’ll talk about the difference between “integrable” and “chaotic” dynamical systems, and the difference between “continuous-time” and “discrete-time” dynamical systems. So we’ll want to fill up this grid with examples:

Continuous-time and integrable

First, let’s consider a :simple pendulum. (Yes, that is the technical term.) This is an object suspended from a string or from a rod that can freely rotate around a hinge. If we give the pendulum a little push, then (ignoring friction) it will keep swinging back and forth again and again.

The graph traced out on the left shows the angle of deflection as a function of time. It is very predictable, and we could write down a formula that precisely describes this graph. The pendulum is an example of an integrable system. “Integrable” is an archaic word for “solvable”: integrable systems are dynamical systems for which we could write down a formula that exactly describes its solution (its state as a function of time). The behaviour of an integrable system is ordered and predictable.

Continuous-time and chaotic

If we attach another pendulum to a simple pendulum, we get a double pendulum. (Yes, that is the technical term.) Let’s give it a good shove and see what happens:

There are now two graphs on the left, representing the angles of both pieces of the pendulum. However, the main difference with the simple pendulum is that these graphs don’t show any repetition or pattern. In fact it is impossible to write down a formula that produces these graphs exactly. Looking at the motion of the system, it is very hard to predict what position it we be in a few seconds into the future. Furthermore, the evolution of the system is :very sensitive to changes in its initial state. These are the properties of a :chaotic system.

You could think of integrable systems and chaotic systems as opposite ends of a wide spectrum representing how dynamical systems can behave.

Discrete-time and chaotic

So far, our systems have evolved :continuously in time: they don’t jump instantaneously from a certain state to a completely different one. There are also systems where it doesn’t make sense to keep track of the configuration at every instant. Consider for example a population of animals that breed once per year, at a fixed time of year. To keep track of the population we don’t need to count them every minute of every day. We can just do one count per year at the end of the breeding season. We can then use this count to predict what the population in the next year will be. Such a model is a discrete-time dynamical system: it takes steps in time of a fixed size.

The following model tracks a population of :rabbits living in a certain habitat with limited resources. If the population is small they all have plenty to eat and will produce large litters. If the population is large they compete for resources and will have smaller litters or even die of starvation. We see that the population fluctuates wildly over the years:

These oscillations do not follow a fixed pattern: sometimes the population grows two years in a row, sometimes its goes up and down in alternating years. This makes it very difficult to predict what will happen a few years in the future. So this discrete-time dynamical system is chaotic.

Discrete-time and integrable

In the next :model the rabbits always have plenty to eat, but they are being hunted by foxes.

If there are only a few foxes, this does not impact the rabbit population very much and it grows quickly. But then, with many rabbits to eat, the foxes do quite well for themselves. After a few years there are so many foxes that a large proportion of the rabbits gets eaten. The rabbit population declines sharply, leaving the large fox population struggling to find food. This causes the fox population to decline, and the cycle starts over.

In this case the oscillations follow a fixed pattern: the population sizes are predictable and we could theoretically write a formula for the graphs they trace. This discrete-time dynamical system is integrable.

Integrable systems are the exception

The simple pendulum is quite, well, simple. Also the predator-prey model describing our rabbits and foxes is much simpler than any realistic ecological model. There are more complicated integrable systems, but they are relatively rare. If a dynamical system is sufficiently complicated, it is usually chaotic. Integrable systems are the exception. Their nice behaviour and predictabillity is due to some :hidden mathematical structure they possess. This structure can take many different forms. There isn’t one type of hidden structure that explains all integrable systems. Studying all these structures and the relations between them is an active are of research.

Many discrete integrable systems have continuous counterparts, and vice versa. Making the connections between discrete and continuous integrable systems precise often sheds light on their hidden structures. :This approach to studying integrable systems is one of the topics of my research.

:Credits

The first two videos are edited screengrabs from https://www.myphysicslab.com.

The last two videos are my own work [source code] made using Manim and public domain images.

Expandable notes are implemented using :Nutshell.

:x Nutshell

These expandable notes are made using :Nutshell ← Click on the : to expand nested nutshells.

:x D S

The mathematical model of anything that moves or changes is called a dynamical system.

:x T T

Yes, that is the technical term.

:x D P

Three double pendulums with near identical initial conditions diverge over time displaying the chaotic nature of the system. [From Wikipedia]

:x C C

In mathematics, a function is “continuous” if small changes in input lead to small changes in output. In the present context we consider the state of a dynamical system as a function of time, so “continuous” means that if we move forward a very small amount of time, then the change in the system’s state will be correspondingly small.

:x B L B

These rabbits don’t breed like bunnies! They can have large litters, yes, but they only reproduce once per year.

:x L V

This is a discrete-time version of the :Lotka-Volterra model.

:x D S I

For readers with a maths background who want to learn more about discrete integrable systems, I recommend the book Discrete Systems and Integrability by J. Hietarinta, N. Joshi and F. W. Nijhoff.

:x L M S

Readers with a maths background who want find out what some of these structures are, could watch for example the 2020 LMS lecture series Introduction to Integrability.

If you’re after more visual representations on integrable systems, check out What is… an integrable system? where I give a different introduction to integrable systems, using waves as examples.

The shapes of waves of ships and ducks

A video about the pattern of waves making up the wake of a ship or a duck. This is a common topic in university-level fluid mechanics courses, but my intention was to give a fairly complete explanation without assuming any more advanced knowledge than trigonometry.

Supplementary material for this video will be added to this pages soon.

Rainbows don’t work the way you think they work

This video on the mathematics behind rainbows communicates visually (without formulas) how the full story is more complicated, but also more beautiful, than “different wavelengths reflect at different angles”.

Below the full video you can find an edited transcript with the individual animations inserted into it. After that there is some additional material on double rainbows.

Full video

Transcript with video snippets

You may already know how a rainbow forms. A key part of the explanation is that sunlight is reflected in raindrops at an angle of about 42 degrees. So we see the reflected light if we are somewhere on this cone of reflected rays.

Put differently, we see reflected light from those droplets that appear to be on an arc, which is centered around the point opposite to the sun. And we don’t see reflected light from any droplets away from this arc.

The angle of reflection is slightly different for different wavelengths of light, which we see as different colours, so instead of one circular arc of reflected sunlight we see a rainbow.

It’s a nice explanation, and not entirely wrong, but the full truth is much more interesting.

Let’s look at what happens within a single raindrop. The sunlight (coming in from the left) is broken, or “refracted”, as it enters the raindrop. Then it is reflected on the inside of the raindrop and finally refracted again when leaving it.

The breaking of light is related the fact that it moves more slowly in water than it does in air. (See this posts about variational principles.) The angle of refraction can be expressed using a formula called Snell’s law.

If you’re confident with trigonometry it’s a good exercise to calculate these angles. We won’t need exact formulas for this explanation to make sense, but if you manage to do this exercise, you’ll notice that the angle of the outbound ray depends on how far from the centre the inbound ray hits the raindrop. The angle, which we denote by $\alpha$ (Greek letter alpha), depends on the distance $ d $ form the centre, as you can see in the animation below.

In hindsight, this shouldn’t be surprising. The angle certainly can’t always be 42°, because if the ray hits the droplet perfectly in the center, it will reflect back exactly the way it came.

It’s true that the angles depend a little on the wavelength of the light too, but the effect of changing the colour is much smaller than the effect of moving to or from the centre.

Let’s focus again on a single colour and draw a graph to visualise the dependence of the angle $\alpha$ on the distance $d$. We start at $d=0$, which means the ray hits at the centre and the angle is zero too. When $d$ increases, at first the angle $\alpha$ increases too. But after a while the graphs flattens out and the angle reaches a maximum. When the ray moves even further from the center, the angle actually becomes smaller again.

We see that, depending on the value of $d$, reflection is possible at any angle up to about 42 degrees.

This is a bit strange, because this seems to imply that a rainbow would be a filled disk in the sky, rather than a circular arc.

A raindisk?? [Background photo: “Morning Rainbow” by Kodyak Tisch, CC BY 2.0]

The reason rainbows look the way they do, is that this graph reaches a maximum value and then goes down again. Whenever a smooth graph has such a maximum, a large portion of the input values will have output values very close to the maximum.

Another way to visualise this, is to look at lot of equally spaced incoming rays hitting our droplet. We see that a disproportionate amount of them reflect at or near the maximum angle.

On the graph these rays correspond to input values evenly distributed over the horizontal axis. After moving them to their output values, we see that the outputs are concentrated near the maximum value. This effect becomes more obvious when we consider more inputs rays.

Up to now we’ve only used light of a single wavelength (ie. of a single colour). The graphs for different wavelengths look very similar, with the notable difference that the maximum value is slightly different for each one. Hence the vertical bars representing our outputs will be of slightly different height, depending on the colour

Sunlight is a mixture of different colours. So what we really want to know is what these coloured bars look like when they overlap. This will give us a visual indication of how much light of which colour is reflected at each angle.

(People say the rainbow has 7 colours, but actually it has infinitely many. We’re using 6 here, which is a reasonable approximation.)

Finally, the light does not only get reflected vertically, but in all directions, so to visualise how the reflections actually look, we need to rotate this coloured bar around its lowest point, which corresponds to the angle zero and would be exactly opposite to where the sun is in the sky.

And voila. Here’s our rainbow. We see the bright arcs of differently coloured light, with a faint mix of colours inside of it, which looks more or less white to us.

So next time you see a shiny rainbow, see if you can tell that the inside of it is slightly brighter than the outside.

Additional material: double rainbows

So far we’ve assumed that the ray reflects exactly once inside the droplet. It could reflect multiple times, or leave the droplet without reflecting.

The most important of these cases is when the ray reflects twice inside the droplet. Let’s have a look at how different incoming rays get deflected in this case.

Again we can construct the graph of outgoing angle as a function of the distance $d$.

This graph has a minimum instead of a maximum, but this will cause the same kind of concentration of outputs near the minimum angle.

Now let’s combine the graph for two reflections with the one for a single reflection and construct the rainbow…

We get a double rainbow with a dark band between the two bows.

In theory, there could also be a triple rainbow, quadruple rainbow, and so one. But with each additional reflection, the rainbow will get dimmer. In addition, the position of the theoretical third rainbow would be quite close to where the sun is, so in practice there is very little chance of ever seeing it.

YouTube video published on 22 August 2021

This page was updated 19 September 2025

The content of this page can be reused with attribution under the CC BY 4.0 license.

What is… a variational principle?

Variational principles play fundamental role in much of mathematical physics and are a key topic in my own research. That’s a lot to cover, so let’s start with a little story…

Variational principles play fundamental role in much of mathematical physics and are a key topic in my own research. That’s a lot to cover, so let’s start with a little story.

1. An injured cow and the laws of physics

On the morning of a hot summer’s day, a farmer noticed that one of his cows had broken its leg out in the field. The unfortunate the animal would not be able to move for a good while. To make sure the cow wouldn’t get dehydrated, the farmer had to bring it water from the stream bordering the field. While the farmer went to fetch a bucket, he thought about the best way to accomplish this task. What would be the shortest route he could take, that first visits the stream and then goes to the cow?

[Image components by OpenClipart-Vectors and Clker-Free-Vector-Images from Pixabay]

It is fairly obvious that the farmer should take a straight line to the river and then another straight line to the cow. We all learned in school that a straight line is the shortest route between two points. But there are still many ways to combine two straight lines into a suitable path. Which point on the river bank should the farmer go to in order to make the path as short as possible?

If you play around with different possibilities for a minute, you might be able to guess that both lines should make the same angle with the river bank. This simple condition, two angles being equal, is all that is needed to determine the shortest path.

The shortest path to the cow, via the river, consists of two straight lines which are at the same angle to the river bank.

A cow with a broken leg is unfortunate, but it could have been worse. What if the cow had fallen into the river? It won’t be able to get back onto dry land with its leg broken. Luckily the river isn’t too deep, so the clumsy animal won’t drown, but the farmer would have to wade into the river to help it.

Now what would be the fastest way for the farmer to reach the cow? The shortest path would be a straight line, but it is safe to assume that the farmer can run through the field faster than he can wade through the stream. So it’s worth taking a slightly longer path if a shorter part of it is in the water. The quickest route might look like this:

The shortest path is a straight line, but the fastest one has a kink.

The problems our farmer is facing are examples of variational problems. We seek to minimize some quantity (distance or time travelled in these examples). If we have found the optimal solution, then any small variation of this solution will be slightly worse. This gives us a first explanation of the name variational problem.

The cows of physics

Why do we care about these problems? It wouldn’t really make a difference if the farmer takes a few seconds more to reach the cow, would it? And taking a slightly longer route probably wastes less time than overthinking the situation. So what’s all the fuss about?

It turns out that physics is a lot like a farmer trying to help his cow.

As a first example, consider a ray of light reflecting in a mirror. Out of all possible paths from the light source, via the mirror, to wherever the ray of light ends up, it will take the shortest. This is because the law of reflection says that the incident ray and the reflected ray will make the same angle with the mirror. And, as our farmer found out, equal angles create the shortest path.

Or is it the other way around? We might say that the law of reflection holds because light always takes the shortest path.

What about the cow in the river? Well, not just the farmer goes slower in water, so does light. It travels at “light speed” (about 300.000 km/s) in vacuum, marginally slower in air, and a lot slower in materials like water or glass. This matters because I lied to you earlier: light doesn’t necessarily take the shortest path, it takes the fastest path. If the speed of light were the same everywhere, this would make no difference. But if different materials are present, then the speed depends on where you are. So, if, for example, a ray of light enters water from the air, it makes a sudden turn. Just like our farmer did to reach his aquatic cow.

An incoming (*“incident”*) ray of light can be reflected at the same angle, or refracted at an angle determined by Snell’s law. In both cases, the angle is such that the light reaches its destination as quick as possible. [Image by Nilok at wikimedia commons]

The phenomenon where light changes direction when it enters a different medium is called refraction. You might have learned the formula for the angle of refraction (known as Snell’s law) in your high school physics class:

$\displaystyle n_i \sin \theta_i = n_R \sin \theta_R.$

But you don’t need to understand this formula, because it just reflects the fact (no pun intended) that light takes the fastest route. If you want to do calculations, you need formulas. But if you want to understand what’s going on, the variational principle is even better. This particular variational principle, that light always takes the quickest path, is called Fermat’s principle.

As we will see below, light is no exception. Many more physical systems are described by variational principles. They are a cornerstone of every part of modern physics. Like many “laws” of physics, the law of reflection and Snell’s law are nothing but consequences of a simple variational principle.

2. Variational principles in statics

Consider an idyllic landscape of rolling hills…

Photo by Jay Huang, https://flic.kr/p/EDy27K

No, wait. Scratch that! Picture these idealized 1-dimensional rolling hills:

The function U gives the height U(x) of the landscape at position x.

The places where a ball would not immediately start rolling down the hill are those where the tangent line to the hill is horizontal: the tops of the hills and the bottoms of the valleys. In terms of calculus, these are the values of $x$ where the derivative of $U$ is zero:

$\displaystyle \frac{\mathrm{d} U(x)}{\mathrm{d} x} = 0$

This leads us to a second interpretation of the word variational. The derivative is the infinitesimal rate of change of a function. We can only have a minimum or a maximum if this rate of change, this variation, is zero. Variational problems look for a situation where the infinitesimal variation of some quantity is zero.

In our 1-dimensional landscape, there are eight such locations. There are eight equilibria, where a ball will stay at rest if there is no external force acting on it:

There is a clear difference between the orange balls and the blue balls. The orange ones are on top of hills. Each of them is at a local maximum of the function $U$. This has the unfortunate consequence that as soon as the ball moves a tiny bit to either side, it will start rolling down the hill, away from its equilibrium. We call these kinds of equilibrium unstable. The blue balls, on the other hand, are at stable equilibria. If a blue ball gets a little kick, it will jiggle about its equilibrium, but eventually it will come back to rest at the same place.

In other words, the variational principle

$\displaystyle \frac{\mathrm{d} U(x)}{\mathrm{d} x} = 0$

determines all equilibria, but if we want to make sure we have a stable equilibrium, we need and additional condition. For example, we could require that the second derivative of $U$ is positive,

$\displaystyle \frac{\mathrm{d}^2 U(x)}{\mathrm{d}^2 x} > 0.$

Both conditions combined guarantee that $U$ has a local minimum at $x$, or, that the ball will be in a stable equilibrium at position $x$.

The function $U$ is called the potential of the system. In this case, where gravity is the only force involved, the potential is essentially the height. In more complex systems, the potential will be a more complicated function of the variables of the system, but its use stays the same. Equilibria are found by applying the variational principle to the potential. Stable equilibria are the local minima of the potential.

3. Variational principles in dynamics

Finding the equilibria of a system is not the whole story. It is good to know where a system can be at rest, but often we also want to understand how it moves when it is not at rest. Miraculously, this is governed by variational principles too.

Suppose we want to keep track of a ball rolling through our 1-dimensional landscape.

We denote the position of the ball at time $t$ by $x(t)$. We can make a graph of position over time, so that $x(t)$ traces out a curve in the $(x,t)$-plane. Most such curves cannot be realized by a ball moving only under the influence of gravity. Those that can be, are called solutions of the system. For each initial position and velocity of the ball, there will be exactly one solution. But how do we find a solution?

Is any of these curves a solution? How can we tell what kind of graph the position of the ball will trace out?

The most common approach is to use Newton’s second law: Force equals mass times acceleration. In a problem like this, at each location $x$ the force $F(x)$ is known. It is determined by the slope of the hill at that position. Acceleration is the second derivative of position with respect to time, so if we know the mass $m$ of the ball, Newton’s second law gives us the formula

$\displaystyle \frac{\mathrm{d}^2 x(t)}{\mathrm{d} t^2} = \frac{F(x)}{m}.$

This is a (second order) differential equation. If the initial position $x(0)$ and the initial velocity $\frac{\mathrm{d} x(t)}{\mathrm{d} t} \Big|_{t=0}$ are given, then it can be solved to determine $x(t)$ for all values of the time $t$. (At least in theory. Only for relatively simple functions $F(x)$ will it be possible to write this solution as a nice formula to calculate $x(t)$.)

Instead of Newton’s second law, we can again use a variational principle. Compared to our previous examples, the quantity we want to minimize is a bit more complicated. Not to worry, though. Once again you don’t need to understand the formula to follow the rest of the text. We want to minimize

$\displaystyle S[x] = \int_0^T \left( \left( \frac{m}{2} \frac{\mathrm{d} x(t)}{\mathrm{d} t} \right)^2 – U(x(t)) \right)\mathrm{d} t,$

where the square brackets $[x]$ indicate that $S$ depends on the function $x$ as a whole, not just on a particular value $x(t)$.

We look for minimizers of $S$ in the following sense. Let the starting position (at time $0$) be $a$ and the final position (at time $T$) $b$, that is $x(0) = a$ and $x(T) = b$. Then $x$ is a solution if $S[x]$ is smaller than $S[y]$ for any other function $y$ with the same boundary values $y(0) = a$ and $y(T) = b$.

With some clever calculations, which involve taking variations of the function $x$, one can see that the functions that minimize $S$ are exactly those that satisfy Newton’s second law. Once again a famous law of physics turns out to be the consequence of a variational principle.

Variational principles are abundant in physics. I’ve only discussed simple examples here, but it turns out that almost all of modern physics can be formulated using variational principles. In fact the easiest way to describe a physical theory is often to write down the thing it minimizes.

Conserved quantities

The story does not end there. Instead of looking at functions with fixed boundary values to obtain Newton’s second Law, we could look only at functions satisfying Newton’s second law but leave the boundary values unspecified. Then similar “clever calculations” give some information about the boundary values. More specifically, they produce conserved quantities, like the energy of the system, which take the same value at the final time as at the initial time (and indeed at any time in between).

Exactly which conserved quantities come out of this procedure depends on the symmetries of the system. Noether’s theorem, named after early 20th century mathematician Emmy Noether, states that every symmetry corresponds to a conserved quantity. For example, if the system is translation invariant (e.g. billiard balls rolling on a plane) then its total momentum is conserved, and if it is rotationally invariant (e.g. planets orbiting the sun) then the angular momentum is conserved.

Knowing conserved quantities of a system helps to understand its dynamics on many levels. Whether you are looking for an exact solution, a numerical approximation, or a qualitative understanding of the behaviour, conserved quantities will always be of use. And if you have read “What is… an integrable system?“, you know that they are the key to a realm of very peculiar dynamical systems.

5. Sources and further reading

As with many concepts related to physics, a good place to start reading are the Feynman lectures: some relevant chapters are Optics: The Principle of Least Time and The Principle of Least Action.

Even though these physical insights (and the maths) have not changed since the Feynman lectures were published over half a century ago, the cutting edge of science communication has moved on. Nowadays there are excellent educational videos on subjects like this.

Most introductory texts on classical mechanics do not give variational principles the attention they deserve. A notable exception (and excellent book) is

Levi, Mark. Classical mechanics with calculus of variations and optimal control: an intuitive introduction. American Mathematical Soc., 2014.

The example of the farmer and the cow is inspired on a problem in

Stankova, Zvezdelina, and Tom Rike, eds. A Decade of the Berkeley Math Circle: The American Experience, Volume II. American Mathematical Soc., 2015.

What is… an integrable system?

The oversimplified answer is that integrable systems are equations with a lot of structure. The kind of equations we are thinking about are differential equations, which describe change. Whenever something is moving, you can count on it that physicists would like to describe it using differential equations.

The oversimplified answer is that integrable systems are equations with a lot of structure.

The kind of equations we are thinking about are differential equations, which describe change. Whenever something is moving, you can count on it that physicists would like to describe it using differential equations. It could be an apple falling from a tree or the earth orbiting the sun, the pendulum of a grandfather clock or the waves carrying your phone signal. Here, we’ll look at water waves.

Playing in the water

Let’s start by throwing a pebble in a pond. If you look carefully at the waves it creates, you’ll see some interesting things. You might observe, for example, that longer waves travel faster than shorter waves. After a while you’ll see a sequence of circular waves that are shorter on the inside and longer on the outside:

This effect, that the speed of a wave depends on the wavelength, is called dispersion. The wake of a boat provides another example:

A second effect that you can observe in the videos above is that the individual wave crests and troughs do not travel at the same speed as the big pattern. The velocity of the individual waves is called the phase velocity, the velocity of the whole pattern is called the group velocity.

Phase velocity (red) and group velocity (green). (Source: http://commons.wikimedia.org/wiki/File:Wave_group.gif)

These examples show typical behaviour of waves. The wave fronts change shape and are torn apart. Compared to the ocean on a stormy day, the waves we’ve seen so far are quite tame, but still things get complicated if we try to understand the details.

Integrability

What we saw above is the way most waves work, but they are not integrable systems. Integrable systems are the exceptions. They are differential equations with solutions that are easy to understand. Integrable wave equations describe waves that are really quite boring.

The waves in an integrable system preserve their shape:

Such a wave is called a soliton, because it occurs by itself and (to theoretical physicists) looks like an elementary particle (particle names often end in -on).

Waves in a narrow and shallow channel like in this video are described by the Kortweg-de Vries equation. This equation is one of the most important examples of an integrable wave equation. The understanding of the Korteweg-de Vries equation as an integrable system dates mostly to the 1960s and 70s, but its history started over a century earlier with a Victorian engineer on horseback chasing a soliton along Scottish canal.

Hidden mathematical structure

Unfortunately “having well-behaved solutions” is not a very good mathematical definition of an integrable system. We want to know the underlying reason why certain equations have nice solution. The explanation is usually some hidden structure.

One type of hidden structure that can make a system integrable is the existence of a large amount of conserved quantities. Like its name suggests, a conserved quantity is something that does not change in time. Most systems in physics have conserve quantities like energy and (angular) momentum, but not many more than those. Integrable systems are those that do have a large number of conserved quantities.

In a way, each conserved quantity is an extra constraint that the system must satisfy: the system must always preserve this quantity. So if there are many conserved quantities, then there are many constraints a solution must fulfil. The Kortweg-de Vries equation has an infinite amount of conserved quantities. Therefore, there are infinitely many constraints that the wave must satisfy. This leaves it with little freedom to change its shape. Initially there might still be some complicated things going on, with smaller waves behaving erratically, but once a large stable wave is formed, it will keep its shape forever.

Conserved quantities are not only part of the explanation of the nice qualitative behaviour we observed, they also help to make quantitative statements about a system. Knowing conserved quantities is very helpful to derive exact solutions of a differential equation. An exact solution is a formula that tells you precisely which shape and position the wave takes at each instant in time. Nowadays we call finding exact solutions “solving” a differential equation, but in the 19th century people would say “integrating” instead. This is where the name integrable system comes from.

Soliton interaction

When two solitons collide, weird stuff happens. Their interaction is complicated and looks a bit chaotic. You’d expect the combined wave to be taller, but actually the height of the crest decreases during the interaction.

But then, magic! After the interaction, the two original waves appear again, as if nothing at all has happened! Even though the waves seem to change during the interaction, the integrable system “remembers” everything about them and in the end they are restored.

One sentence about my work

My research involves a relatively new approach to integrable systems, which is to describe them using variational principles.

You can find out here what a variational principle is. Or, if you’ve had enough maths for one day, you can head to Gloucestershire instead and try to surf a soliton:

You can find a more technical introduction
to integrable systems in these slides